
Stochastic homogenization: PDEs with random coefficients
Homogenization - the derivation of effective large-scale descriptions of materials which are heterogeneous on small scales - has been a very influential field of analysis during the last decades. The predictions of classical homogenization, however, are often restricted to periodically varying materials. Unfortunately, materials occuring in nature are almost never perfectly periodic; rather, the microscopic material properties are expected to be somewhat randomly distributed and the correlations of the microscopic properties of the material are expected to decay on larger scales. It is a basic observation of stochastic homogenization that nevertheless a homogenization result holds in many cases. Despite the qualitative theory for stochastic homogenization of e.g. elliptic equations having been settled decades ago, the quantitative theory is a very active area of research.
In a recent joint work with Stefan Neukamm [25], we have derived the first optimal-order homogenization error estimates for nonlinear elliptic PDEs with random material law. Another recent work is concerned with the rigorous justification of a selection approach for representative volumes proposed by Le Bris, Legoll, and Minvielle: In stochastic homogenization, the effective material law is typically determined by evaluating the cell formula on a sample of the random material, the so-called representative volume. It has been observed numerically by Le Bris et al that selecting a sample which is particularly representative for the material may increase the accuracy substantially. In [19, 21], we have developed a rigorous analysis of this approach.
Further results of our research include a proof of a higher-order rate of convergence in weak norms for linear elliptic PDEs with random coefficient field ([16], jointly with Peter Bella, Benjamin Fehrman, and Felix Otto), a Ck,α large-scale regularity theory and associated Liouville principles for random elliptic operators ([12], jointly with Felix Otto), and the analysis of numerical homogenization schemes ([24], jointly with Dietmar Gallistl and Daniel Peterseim).
Publications: [12, 13, 14, 16, 19, 21, 24, 25, 26, 29, 30, P5, P6]
Homogenization - the derivation of effective large-scale descriptions of materials which are heterogeneous on small scales - has been a very influential field of analysis during the last decades. The predictions of classical homogenization, however, are often restricted to periodically varying materials. Unfortunately, materials occuring in nature are almost never perfectly periodic; rather, the microscopic material properties are expected to be somewhat randomly distributed and the correlations of the microscopic properties of the material are expected to decay on larger scales. It is a basic observation of stochastic homogenization that nevertheless a homogenization result holds in many cases. Despite the qualitative theory for stochastic homogenization of e.g. elliptic equations having been settled decades ago, the quantitative theory is a very active area of research.
In a recent joint work with Stefan Neukamm [25], we have derived the first optimal-order homogenization error estimates for nonlinear elliptic PDEs with random material law. Another recent work is concerned with the rigorous justification of a selection approach for representative volumes proposed by Le Bris, Legoll, and Minvielle: In stochastic homogenization, the effective material law is typically determined by evaluating the cell formula on a sample of the random material, the so-called representative volume. It has been observed numerically by Le Bris et al that selecting a sample which is particularly representative for the material may increase the accuracy substantially. In [19, 21], we have developed a rigorous analysis of this approach.
Further results of our research include a proof of a higher-order rate of convergence in weak norms for linear elliptic PDEs with random coefficient field ([16], jointly with Peter Bella, Benjamin Fehrman, and Felix Otto), a Ck,α large-scale regularity theory and associated Liouville principles for random elliptic operators ([12], jointly with Felix Otto), and the analysis of numerical homogenization schemes ([24], jointly with Dietmar Gallistl and Daniel Peterseim).
Publications: [12, 13, 14, 16, 19, 21, 24, 25, 26, 29, 30, P5, P6]
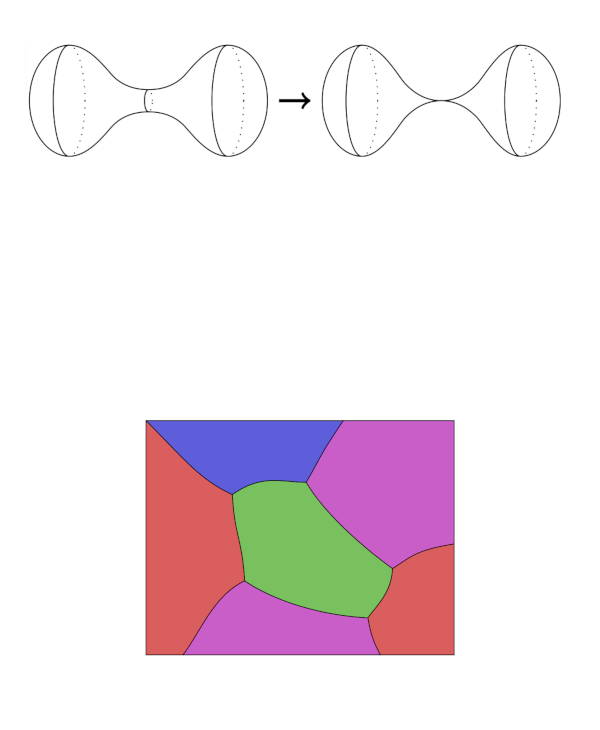
Interface evolution problems
In evolution equations for interfaces, topological changes and geometric singularities often occur naturally, one basic example being the pinchoff of liquid droplets. As a consequence, strong solution concepts for such PDEs are naturally limited to short-time existence results or particular initial configurations like perturbations of a steady state. At the same time, the transition from strong to weak solution concepts for PDEs is prone to incurring unphysical non-uniqueness of solutions. In the absence of a comparison principle, the relation between weak and strong solution concepts for interface evolution problems has remained a mostly open question. We have recently derived a weak-strong uniqueness principle for varifold solutions to the free boundary problem for the Navier-Stokes equation for two immiscible incompressible fluids ([20], jointly with Sebastian Hensel). In other words, the weak solution concept of varifold solutions does not allow for unphysical solutions prior to the formation of geometric singularities.
In a recent work, we have succeeded in proving uniqueness of BV solutions to multiphase mean curvature flow in the plane prior to the first topology change ([31], jointly with Sebastian Hensel, Tim Laux, and Theresa Simon). Our approach is based on the development of a gradient-flow analogue of the concept of calibrations, providing information about the local structure of the energy landscape near a classical evolution.
The relative energy approach to interface evolution problems also has important applications in the analysis of sharp-interface limits: In [22], we give a short proof of just 11 pages for the quantitative convergence of the Allen-Cahn equation towards (two-phase) mean curvature flow. In [34] (joint work with Alice Marveggio), we give the first proof of quantitative convergence of the vectorial Allen-Cahn equation towards multiphase mean curvature flow.
Publications: [20, 22, 31, 34]
In evolution equations for interfaces, topological changes and geometric singularities often occur naturally, one basic example being the pinchoff of liquid droplets. As a consequence, strong solution concepts for such PDEs are naturally limited to short-time existence results or particular initial configurations like perturbations of a steady state. At the same time, the transition from strong to weak solution concepts for PDEs is prone to incurring unphysical non-uniqueness of solutions. In the absence of a comparison principle, the relation between weak and strong solution concepts for interface evolution problems has remained a mostly open question. We have recently derived a weak-strong uniqueness principle for varifold solutions to the free boundary problem for the Navier-Stokes equation for two immiscible incompressible fluids ([20], jointly with Sebastian Hensel). In other words, the weak solution concept of varifold solutions does not allow for unphysical solutions prior to the formation of geometric singularities.
In a recent work, we have succeeded in proving uniqueness of BV solutions to multiphase mean curvature flow in the plane prior to the first topology change ([31], jointly with Sebastian Hensel, Tim Laux, and Theresa Simon). Our approach is based on the development of a gradient-flow analogue of the concept of calibrations, providing information about the local structure of the energy landscape near a classical evolution.
The relative energy approach to interface evolution problems also has important applications in the analysis of sharp-interface limits: In [22], we give a short proof of just 11 pages for the quantitative convergence of the Allen-Cahn equation towards (two-phase) mean curvature flow. In [34] (joint work with Alice Marveggio), we give the first proof of quantitative convergence of the vectorial Allen-Cahn equation towards multiphase mean curvature flow.
Publications: [20, 22, 31, 34]
Entropic reaction-diffusion equations
For many chemical reactions occurring in nature, the reaction rate is approximated well by mass-action kinetics. However, in reaction rates of mass-action type, possibly large powers of the species densities enter. At the same time, only limited energy estimates are available for the corresponding reaction-diffusion equation. For this reason, for reaction-diffusion equations with species-dependent diffusion and mass-action kinetics in general no global existence of any kind of solution was known. In [8], I have proposed a notion of renormalized solution for such equations; relying on the entropy inequality, global existence of solutions is proven. If a posteriori the reaction rates turn out to be integrable, this notion of renormalized solution reduces to the usual notion of weak solution [15]. Currently, we are developing a corresponding existence theory for temperature-dependent reaction-diffusion equations.
Publications: [8, 15, 27, 32, P2]
For many chemical reactions occurring in nature, the reaction rate is approximated well by mass-action kinetics. However, in reaction rates of mass-action type, possibly large powers of the species densities enter. At the same time, only limited energy estimates are available for the corresponding reaction-diffusion equation. For this reason, for reaction-diffusion equations with species-dependent diffusion and mass-action kinetics in general no global existence of any kind of solution was known. In [8], I have proposed a notion of renormalized solution for such equations; relying on the entropy inequality, global existence of solutions is proven. If a posteriori the reaction rates turn out to be integrable, this notion of renormalized solution reduces to the usual notion of weak solution [15]. Currently, we are developing a corresponding existence theory for temperature-dependent reaction-diffusion equations.
Publications: [8, 15, 27, 32, P2]
Thin liquid films and free boundary problems
The thin-film equation describes the surface-tension-driven evolution of thin viscous liquid films on a solid surface. Mathematically, it is a fourth-order degenerate parabolic equation. The analysis of free boundaries in solutions to the thin-film equation is a difficult issue: For a long time, only upper bounds on free boundary propagation have been available. Due to a lack of a comparison principles for higher-order equations like the thin-film equation, standard strategies for the derivation of lower bounds on free boundary propagation do not apply. My discovery of certain monotonicity formulas for solutions to the thin-film equation has provided better insights, resulting in optimal sufficient conditions for instantaneous forward motion of the free boundary and optimal lower bounds on asymptotic propagation rates for the free boundary. The resulting method turned out to be flexible enough to allow for analysing qualitative behaviour of solutions to other higher-order parabolic equations.
Publications: [3, 5, 6, 11, 17, 23, 24, 28, P1]
The thin-film equation describes the surface-tension-driven evolution of thin viscous liquid films on a solid surface. Mathematically, it is a fourth-order degenerate parabolic equation. The analysis of free boundaries in solutions to the thin-film equation is a difficult issue: For a long time, only upper bounds on free boundary propagation have been available. Due to a lack of a comparison principles for higher-order equations like the thin-film equation, standard strategies for the derivation of lower bounds on free boundary propagation do not apply. My discovery of certain monotonicity formulas for solutions to the thin-film equation has provided better insights, resulting in optimal sufficient conditions for instantaneous forward motion of the free boundary and optimal lower bounds on asymptotic propagation rates for the free boundary. The resulting method turned out to be flexible enough to allow for analysing qualitative behaviour of solutions to other higher-order parabolic equations.
Publications: [3, 5, 6, 11, 17, 23, 24, 28, P1]
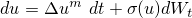
Stochastic partial differential equations
Stochastic partial differential equations are an important tool in mathematical modeling. However, for many methods for deterministic PDE, no counterparts for SPDE have yet been established. In a joint work with Günther Grün [7], we devised a technique for proving upper bounds on the expansion of the support of solutions to degenerate parabolic stochastic PDE, resulting in sufficient conditions for the occurrence of a waiting time phenomenon for the stochastic porous medium equation.
In a recent line of reseach, we aim to provide a rigorous justification of SPDE models from fluctuating hydrodynamics. Our first result in this direction ([33], joint work with Federico Cornalba) is concerned with the Dean-Kawasaki equation, an SPDE for density fluctuations in systems of diffusing particles. We prove that the Dean-Kawasaki equation accurately predicts the law of fluctuations in systems of diffusing particles, with an error of high order in the number of particles.
Publications: [7, 17, 33]
Stochastic partial differential equations are an important tool in mathematical modeling. However, for many methods for deterministic PDE, no counterparts for SPDE have yet been established. In a joint work with Günther Grün [7], we devised a technique for proving upper bounds on the expansion of the support of solutions to degenerate parabolic stochastic PDE, resulting in sufficient conditions for the occurrence of a waiting time phenomenon for the stochastic porous medium equation.
In a recent line of reseach, we aim to provide a rigorous justification of SPDE models from fluctuating hydrodynamics. Our first result in this direction ([33], joint work with Federico Cornalba) is concerned with the Dean-Kawasaki equation, an SPDE for density fluctuations in systems of diffusing particles. We prove that the Dean-Kawasaki equation accurately predicts the law of fluctuations in systems of diffusing particles, with an error of high order in the number of particles.
Publications: [7, 17, 33]
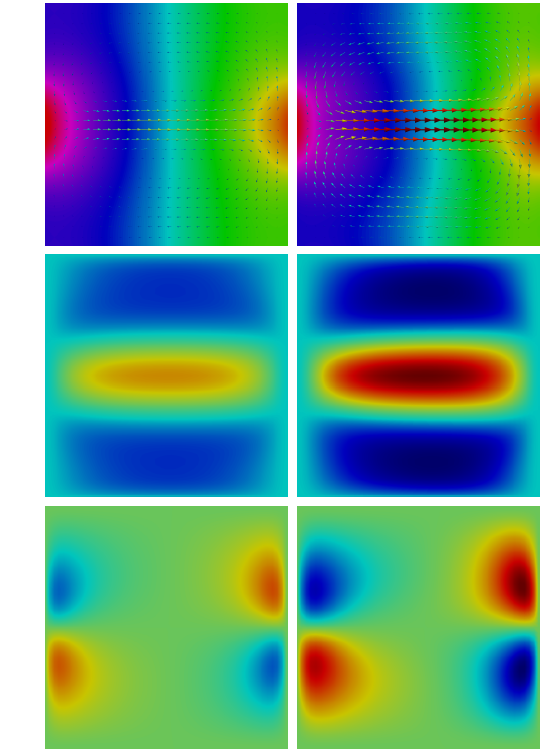
A posteriori modeling error estimates in fluid mechanics
Models in continuum mechanics - like e.g. the Navier-Stokes equation - in general arise by a drastic simplification of reality. Most model simplification steps rely on modeling assumptions, whose validity is sometimes questionable also in practical situations. As the breakdown of the modeling assumptions may invalidate the predictions of the simplified model, rigorous estimates for the modeling error are highly desirable. In [9], I have derived fully rigorous explicit a posteriori estimates for the modeling error caused by the approximation of a slightly compressible fluid as perfectly incompressible, i.e. for the approximation of the compressible Navier-Stokes equation by the incompressible Navier-Stokes equation. My estimates hold for weak solutions to the compressible Navier-Stokes equation as constructed by Lions without assuming any additional regularity. In a subsequent work, I have derived a posteriori modeling error estimates for the higher-order approximation of the compressible Navier-Stokes equation by the combination of the incompressible Navier-Stokes equation with the equations of linearized acoustics. The general approach of a posteriori modeling error estimates - using the information provided by the precise (exact or numerical) solution to the simplified model in order to justify the model simplification a posteriori - is also a promising field for future research, with many questions in particular in fluid mechanics being yet to be settled.
Publications: [9, P3]
Models in continuum mechanics - like e.g. the Navier-Stokes equation - in general arise by a drastic simplification of reality. Most model simplification steps rely on modeling assumptions, whose validity is sometimes questionable also in practical situations. As the breakdown of the modeling assumptions may invalidate the predictions of the simplified model, rigorous estimates for the modeling error are highly desirable. In [9], I have derived fully rigorous explicit a posteriori estimates for the modeling error caused by the approximation of a slightly compressible fluid as perfectly incompressible, i.e. for the approximation of the compressible Navier-Stokes equation by the incompressible Navier-Stokes equation. My estimates hold for weak solutions to the compressible Navier-Stokes equation as constructed by Lions without assuming any additional regularity. In a subsequent work, I have derived a posteriori modeling error estimates for the higher-order approximation of the compressible Navier-Stokes equation by the combination of the incompressible Navier-Stokes equation with the equations of linearized acoustics. The general approach of a posteriori modeling error estimates - using the information provided by the precise (exact or numerical) solution to the simplified model in order to justify the model simplification a posteriori - is also a promising field for future research, with many questions in particular in fluid mechanics being yet to be settled.
Publications: [9, P3]

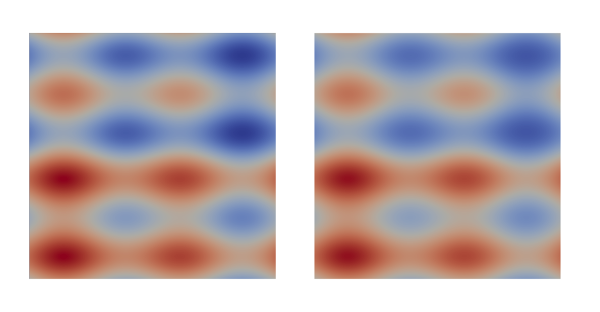
Quantum drift-diffusion models
In a certain regime, the process of charge transport in semiconductors can approximately be captured by drift-diffusion models. A refined version of the classical drift-diffusion models are the so-called quantum drift-diffusion models, which incorporate extra terms accounting for quantum corrections. The question of existence of solutions to the resulting PDEs was settled more than half a decade ago; however, in the nonstationary case the question of uniqueness of solutions has since remained open. In [4], I have succeeded in proving uniqueness of solutions and even well-posedness of the problem. By an adaption of the method developed for the thin-film equation, I have also shown infinite speed of propagation of solutions.
Publications: [2, 4]
In a certain regime, the process of charge transport in semiconductors can approximately be captured by drift-diffusion models. A refined version of the classical drift-diffusion models are the so-called quantum drift-diffusion models, which incorporate extra terms accounting for quantum corrections. The question of existence of solutions to the resulting PDEs was settled more than half a decade ago; however, in the nonstationary case the question of uniqueness of solutions has since remained open. In [4], I have succeeded in proving uniqueness of solutions and even well-posedness of the problem. By an adaption of the method developed for the thin-film equation, I have also shown infinite speed of propagation of solutions.
Publications: [2, 4]